Microsegregation

Dr. Dmitri Kopeliovich

Solidification of a liquid alloy is characterized by a phenomenon called segregation.

Segregation is a separation of impurities and alloying elements in different regions of solidified alloy.

Segregation is caused by the rejection of the solutes from a solidified alloy into the liquid phase. This rejection is a result of different solubility of impurities in liquid and solid phases at the equilibrium temperature.

Segregation may be illustrated by a phase diagram.



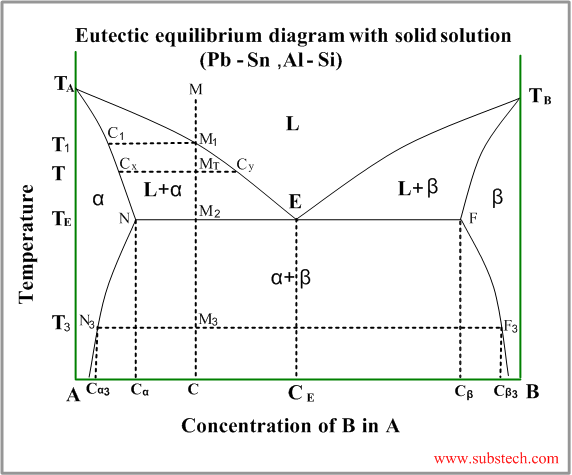
Consider solidification of an alloy with concentration C.
When the temperature reaches the value T_L (point M₁ on the liquidus curve) solidification starts. According to solidus curve the first solid crystals (primary crystals) of the α-phase have composition C₁.
Further cooling of the alloy causes changing of the liquid phase composition according to the liquidus curve and when the alloy temperature reaches a certain intermediate value T (position M_T ), liquid phase of composition C_L=C_y and solid α-phase of composition C_S=C_x are in equilibrium.

If the liquidus and solidus curves are close to straight lines the relationship between the solid and liquid compositions in equilibrium may be described by the Equilibrium Partition Coefficient:

K = C_S/C_L

Solid phase forming during solidification has a form of dendrites. According to the above equation the solid dendrite arms have low content of solutes when the liquid phase locating in the spaces between the dendrite arms is enriched by the solutes.
Partition of solutes between the dendrite arms and interdendritic liquid is called microsegregation.

Microsegregation of solutes in a progressively solidifying alloy may be calculated by means of the following equations:

• Scheil’s equation

Scheil’s equation assumes complete mixing of the liquid phase and no diffusion in solid phase.

C_S = K*C₀*(1-f_S)^K-1

C_L = C₀*f_L)^K-1 = C₀*(1-f_S)^K-1

where:
C_S - concentration of solutes in solid phase adjacent to the solid-liquid boundary;
f_S, f_L - fractions of solid and liquid phases in the solidifying alloy;
C₀ - total concentration of the solute in the alloy.

• Modified Scheil’s equation

Brody and Flemings modified Scheil’s equation by taking into account diffusion in solid dendrite arms:

C_S = K*C₀*(1-f_S/(1+α*K))^K-1

α = 4D_St_f/d²

where:
D_S - diffusion coefficient of the solute in solid alloy;
t_f - time of local crystallization;
d - distance between the dendrite arms.
to top

• Solidification
• Phase transformations and phase diagrams
• Basic principles of heat treatment
• Plastic deformation
• Crystallization
• Foundry technologies
• Macrosegregation in steel ingots

to Metals
to Basic processes in metals